Redis详解(三):布隆过滤器

小管

Redis

发布于：Apr 28, 2021

次浏览

3k words

10 min

0  

一、概述

我们假设一种场景:刷抖音

你有刷到过重复的推荐内容吗?这么多的推荐内容要推荐给这么多的用户,他是怎么保证每个用户在看推荐内容时,保证不会出现之前已经看过的推荐视频呢?也就是说,抖音时如何实现推送去重的呢?

你会想到服务器 记录 了用户看过的 所有历史记录,当推荐系统推荐短视频时会从每个用户的历史记录里进行 筛选,过滤掉那些已经存在的记录.问题是当 用户量很大,每个用户看过的短视频又很多的情况下,这种方式,推荐系统的去重工作 在性能上跟的上么？

实际上,如果历史记录存储在关系数据库里,去重就需要频繁地对数据库进行 exists 查询,当系统并发量很高时,数据库是很难抗住压力的.

你可能又想到了 缓存,但是这么多用户这么多的历史记录,如果全部缓存起来,那得需要 浪费多大的空间 啊.. (可能老板看一眼账单,看一眼你..) 并且这个存储空间会随着时间呈线性增长,就算你用缓存撑得住一个月,但是又能继续撑多久呢？不缓存性能又跟不上,咋办呢？

布隆过滤器(Bloom Filter) 就是这样一种专门用来解决去重问题的高级数据结构.但是跟 HyperLogLog 一样,它也一样有那么一点点不精确,也存在一定的误判概率,但它能在解决去重的同时,在 空间上能节省 90% 以上,也是非常值得的.

1.1 什么是布隆过滤器

布隆过滤器（Bloom filter）是一种非常节省空间的概率数据结构（space-efficient probabilistic data structure）,运行速度快（时间效率）,占用内存小（空间效率）,但是有一定的误判率且无法删除元素.本质上由一个很长的二进制向量和一系列随机映射函数组成.

1.2 布隆过滤器特性

• 检查一个元素是否在集成中;
• 检查结果分为2种：一定不在集合中、可能在集合中;
• 布隆过滤器支持添加元素、检查元素,但是不支持删除元素;
• 检查结果的“可能在集合中”说明存在一定误判率;
  • 已经添加进入布隆过滤器的元素是不会被误判的,仅未添加过的元素才可能被误判;
• 相比set、Bitmaps非常节省空间：因为只存储了指纹信息,没有存储元素本身;
• 添加的元素超过预设容量越多,误报的可能性越大.

需要注意的是,虽然使用了无偏hash函数,使得hash值尽可能均匀,但是不同的item计算出的hash值依旧可能重复,所以布隆过滤器返回元素存在,实际是有可能不存在的.

二、布隆过滤器原理解析

布隆过滤器本质上是由长度为m的位向量或位列表（仅包含 0 或 1 位值的列表）组成,最初所有的值均设置为 0,所以我们先来创建一个稍微长一些的位向量用作展示：

当我们向布隆过滤器中添加数据时,会使用 多个 hash 函数对 key 进行运算,算得一个证书索引值,然后对位数组长度进行取模运算得到一个位置,每个 hash 函数都会算得一个不同的位置.再把位数组的这几个位置都置为 1 就完成了 add 操作,例如,我们添加一个 wmyskxz：

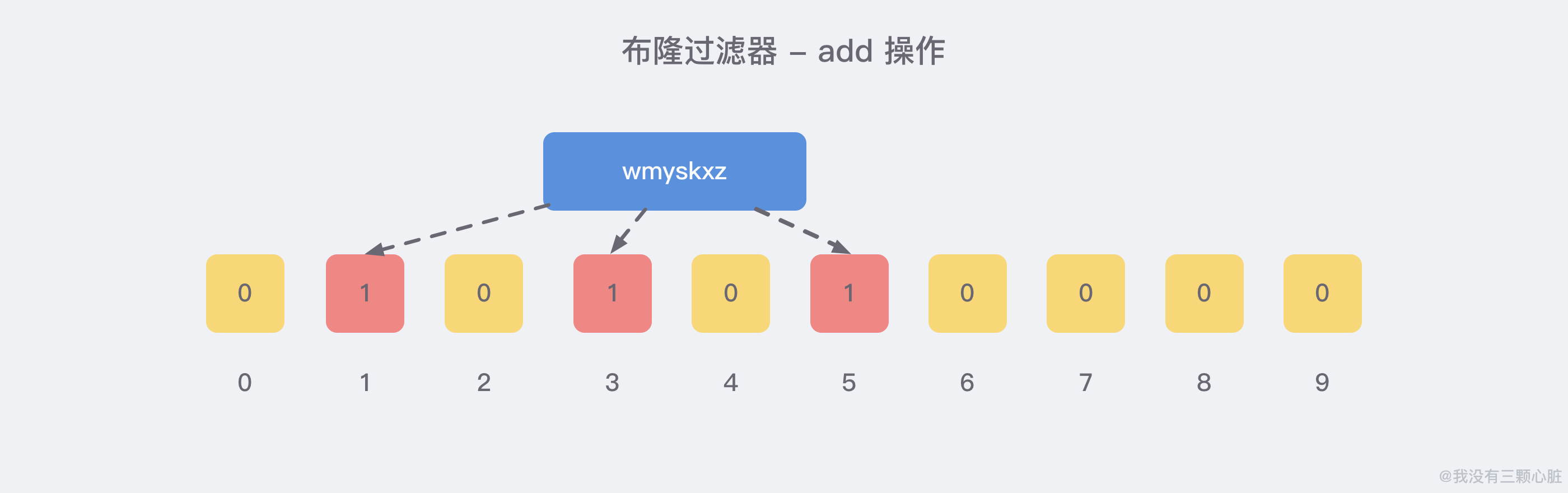
向布隆过滤器查查询 key 是否存在时,跟 add 操作一样,会把这个 key 通过相同的多个 hash 函数进行运算,查看 对应的位置 是否 都 为 1,只要有一个位为 0,那么说明布隆过滤器中这个 key 不存在.如果这几个位置都是 1,并不能说明这个 key 一定存在,只能说极有可能存在,因为这些位置的 1 可能是因为其他的 key 存在导致的.

就比如我们在 add 了一定的数据之后,查询一个 不存在 的 key：

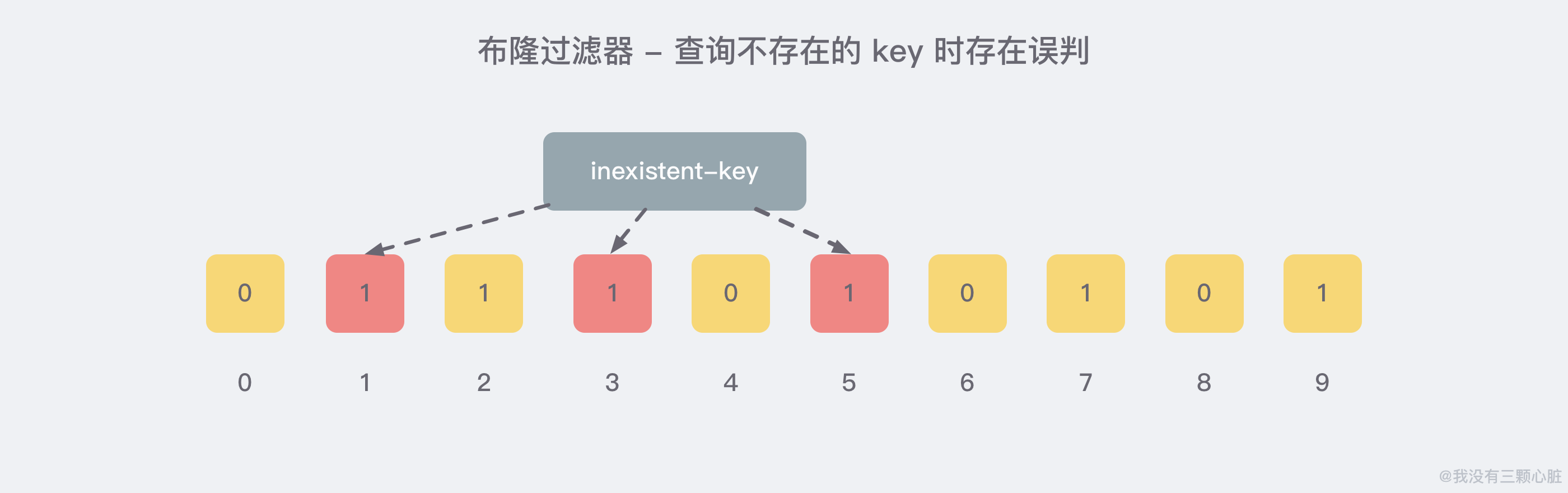
很明显,1/3/5 这几个位置的 1 是因为上面第一次添加的 wmyskxz 而导致的,所以这里就存在 误判.幸运的是,布隆过滤器有一个可以预判误判率的公式,比较复杂,感兴趣的朋友可以自行去阅读,比较烧脑.. 只需要记住以下几点就好了：

• 使用时 不要让实际元素数量远大于初始化数量;
• 当实际元素数量超过初始化数量时,应该对布隆过滤器进行 重建,重新分配一个 size 更大的过滤器,再将所有的历史元素批量 add 进行;

三、布隆过滤器底层原理

3.1 布隆过滤器的底层结构

布隆过滤器本质是一个巨大的bit数组（bit array）+几个不同的无偏hash函数.

  布隆过滤器添加一个item(“gleaming”),其操作步骤是：

• 使用多个无偏哈希函数对item进行hash运算,得到多个hash值hash(gleaming);
• 每个hash值对bit数组取模得到位数组中的位置index(gleaming);
• 判断所有index位是否都为1 ;
• 位都为1则说明该元素可能已经存在了;
• 任意一位不为1则说明一定不存在,此时会将不为1的位置为1;

需要注意的是,虽然使用了无偏hash函数,使得hash值尽可能均匀,但是不同的item计算出的hash值依旧可能重复,所以布隆过滤器返回元素存在,实际是有可能不存在的.

3.2 最佳hash函数数量与错误率的关系

源码中计算hash函数数量的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

# hash函数数量计算公式：

# ceil(value)：返回不小于value的最小整数；
# log(error)：以10为底的对数函数；
# ln(x)：以e为底的对数函数；
# ln(2) ≈ 0.693147180559945;
# ln(2)^2 ≈ 0.480453013918201;

bloom->hashes = (int)ceil(0.693147180559945 * bloom->bpe);

static double calc_bpe(double error) {
    static const double denom = 0.480453013918201; // ln(2)^2
    double num = log(error);

    double bpe = -(num / denom);
    if (bpe < 0) {
        bpe = -bpe;
    }
    return bpe;
}

3.3 所需存储空间与错误率及容量的关系

占用内存（单位M） = bytes值/1024/1024.

  从上述对比分析可以看出,错误率{error_rate}越小,所需的存储空间越大; 初始化设置的元素数量{capacity}越大,所需的存储空间越大,当然如果实际远多于预设时,准确率就会降低.

  在1千万数据场景下,error_rate为0.001、0.0001、0.00001实际占用内存都是30M以下,此时如果对准确性要求高,初始化时将错误率设置低一点是完全无伤大雅的.

  RedisBloom官方默认的error_rate是 0.01,默认的capacity是 100,源码如下：

1
2
3
4

// RedisBloom/src/rebloom.c

static double BFDefaultErrorRate = 0.01;
static size_t BFDefaultInitCapacity = 100;

四、布隆过滤器的应用场景

4.1 邮件黑名单&网站黑名单

邮箱地址数十亿计且长度不固定,我们需要从海量的邮箱地址中识别出垃圾邮箱地址.当一个邮箱地址被判定为垃圾邮箱后,就将此地址添加进布隆过滤器中即可.

  同理,万维网上的URL地址中包含了大量的非法或恶意URL,利用布隆过滤器也可以快速判断此类URL.当布隆过滤器返回结果为存在时,才对URL进行进一步判定处理.

4.2 新闻去重

对于百度新闻、头条新闻等信息推荐平台,为了尽可能提升用户体验,应最大可能保证推荐给用户的新闻不重复,将已推荐给用户的文章ID存入布隆过滤器,再次推荐时先判断是否已推送即可.

4.3 缓存穿透&恶意攻击

缓存穿透：是指查询了缓存和数据库中都没有的数据.当此类查询请求量过大时（比如系统被恶意攻击）,缓存系统或数据库的压力将增大,极容易宕机.

  方式1：当查询DB中发现某数据不存在时,则将此数据ID存入布隆过滤器,每次查询时先判断是否存在于布隆过滤器,存在则说明数据库无此数据,无需继续查询了.当然此种方式仅能处理同一个ID重复访问的场景.

  方式2：如果攻击者恶意构造了大量不重复的且数据库中不存在的数据呢,此时可将数据库中已有的数据的唯一ID放入布隆过滤器,每次查询时先判断是否存在于布隆过滤器,存在才调用后端系统查询,则可有效过滤恶意攻击.

  使用方式1需要防止指定ID最初不存在于DB中,遂将此ID存入“数据不存在的过滤器”中,但后续DB又新增了此ID,因为布隆过滤器不支持删除操作,一旦发生此类场景,就肯定会出现误判了.

  使用方式2需要注意数据的增量,避免数据库中新增了数据而过滤器中还没有导致无法查询到数据.当然如果此时DB中删除了指定数据,布隆过滤器是无法随之删除指纹标记的.

  了解了原理方能如臂使指.此外建议,生产数据的ID应定义生成规则及校验规则（比如身份证的最后一位就是校验位）,这样每次查询先判断这个ID是否有效,有效才进行后续的步骤,这样可以充分过滤外部的恶意攻击.

五、布隆过滤器的优缺点

5.1 布隆过滤器的优点

• 【适合大数据场景】：支持海量数据场景下高效判断元素是否存在;
• 【节省空间】：不存储数据本身,仅存储hash结果取模运算后的位标记;
• 【数据保密】：不存储数据本身,适合某些保密场景;

5.2 布隆过滤器的缺点

• 误判】：由于存在hash碰撞,匹配结果如果是“存在于过滤器中”,实际不一定存在;
• 【不可删除】：没有存储元素本身,所以只能添加但不可删除;
• 【空间利用率不高】：创建过滤器时需提前预估创建,当错误率越低时,为了尽可能避免hash碰撞,冗余的空间就越多;需要注意的是,空间利用率不高和节省空间并不冲突;
• 【容量满时误报率增加】当容量快满时,hash碰撞的概率变大,插入、查询的错误率也就随之增加了.

5.3 布隆过滤器的其他问题

• 【不支持计数】：同一个元素可以多次插入,但效果和插入一次相同;
• 【查询速度受错误率影响】：由于错误率影响hash函数的数量,当hash函数越多,每次插入、查询需做的hash操作就越多;

更新于：Jul 28, 2022